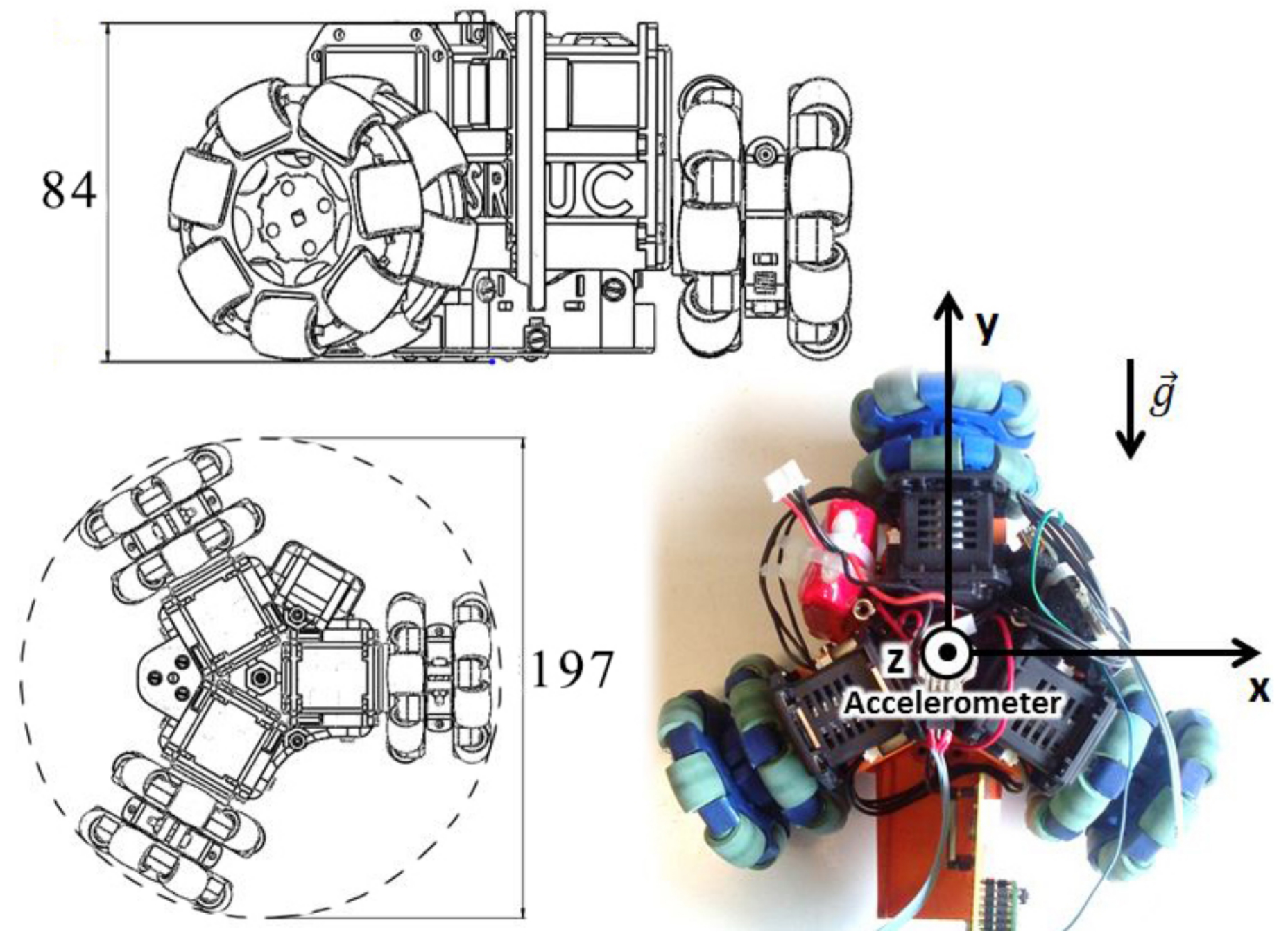
OmniClimber-VI, showing dimensions and reference axis.

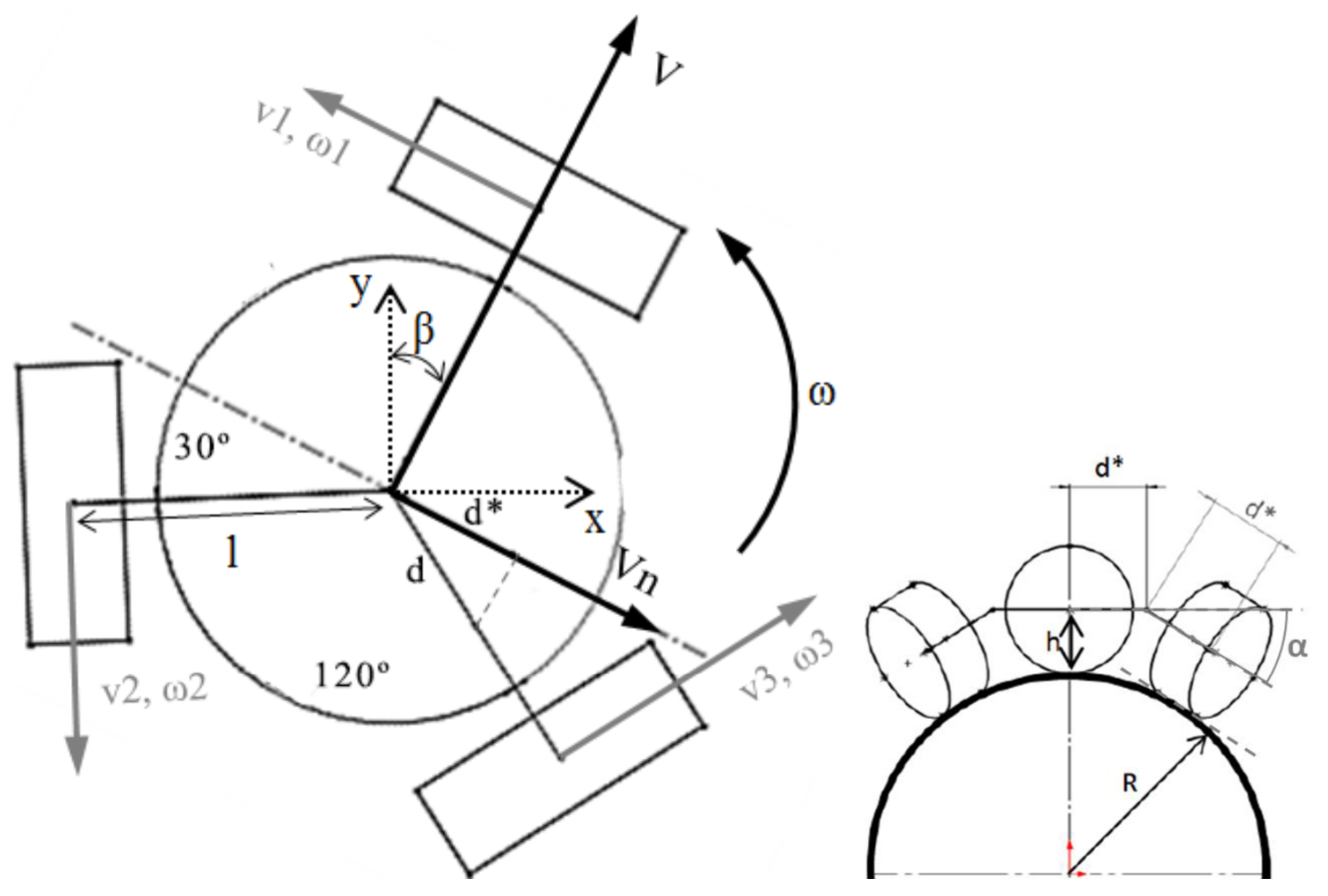
Kinematics model of the 3 wheeled omnidirectional platform with representation of relevant axis and velocities. Notation: x, y – static world axis; β – Yaw angle [rad]; l – distance between the wheels and center of the robot [m]; v1, v2, v3 – wheels linear velocity [m/s]; ω1, ω2, ω3 – wheels angular velocity [rad/s]; V, V n – robot front and lateral velocity [m/s]; ω – robot angular velocity [rad/s]; α – Bending angle of the arms [rad]; R – radius of the structure [m]; h – height of the CG of the robot (roughly equal to the radius of the omnidirectional wheel) [m]; d – half length of the robot arm [m];

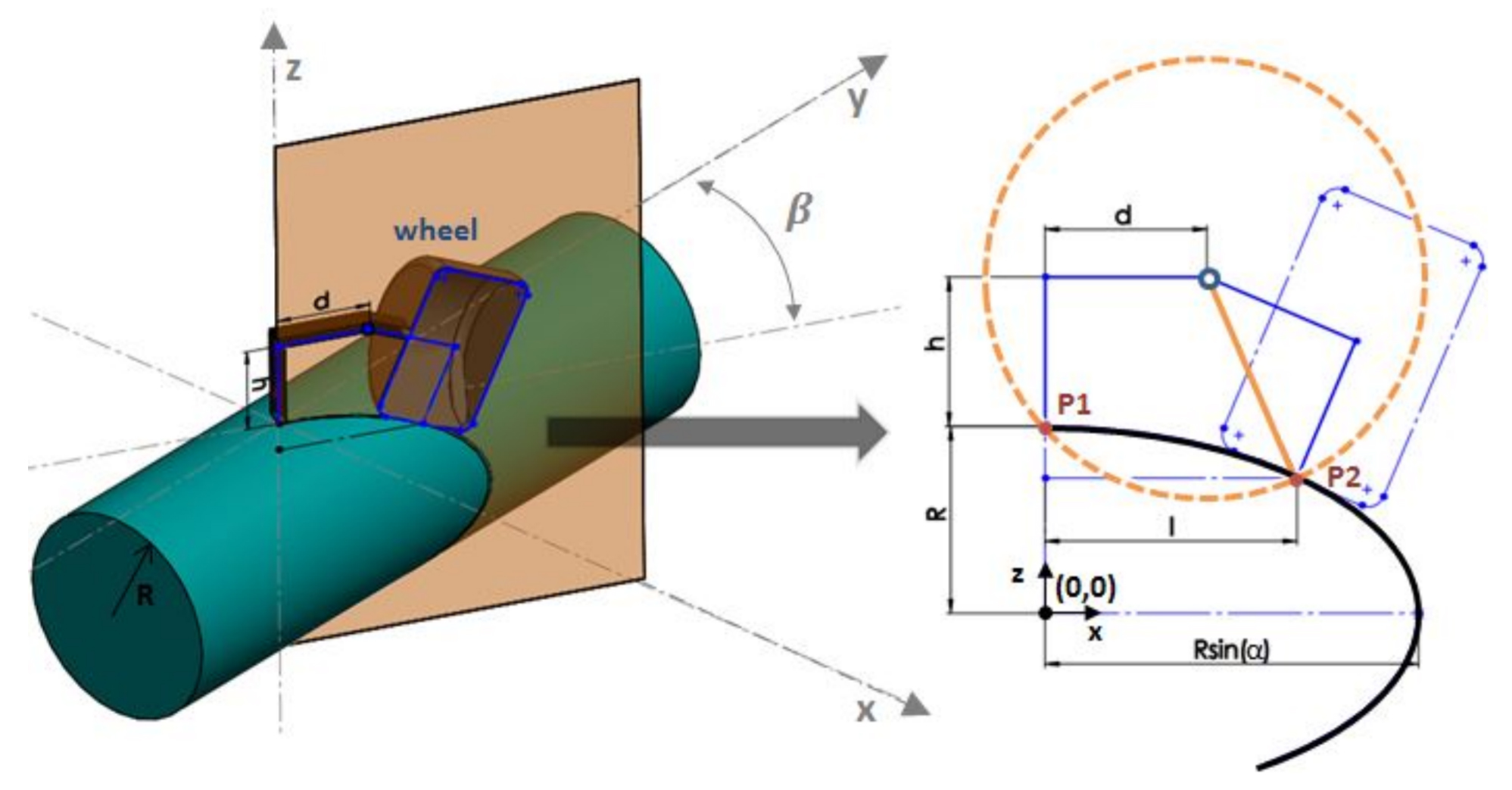
Geometric relations used to determine the distance l between the point of contact (POC) with the surface and the center of the robot. Notation: x, y, z – static world axis; β – Yaw angle [rad]; R – radius of the structure [m]; h – height of the CG of the robot (roughly equal to the radius of the omnidirectional wheel) [m]; d – half of the robot arm length [m]; l – distance between the wheel POC and center of the robot [m];

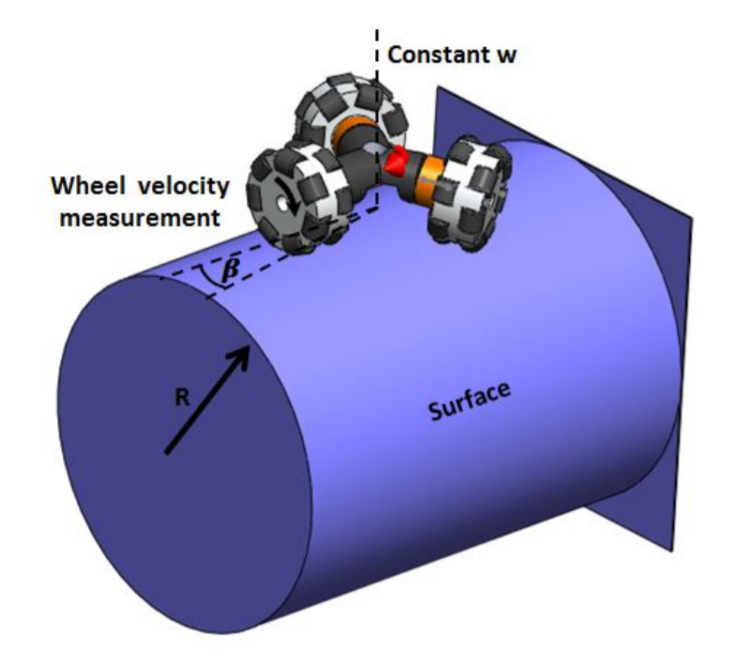
3D simulation for new kinematic model validation.

Snapshots from the Omniclimber experiments on a pole of 220mm diameter, without and with the new controller. Rotating around the pole while keeping the robots orientation constant.

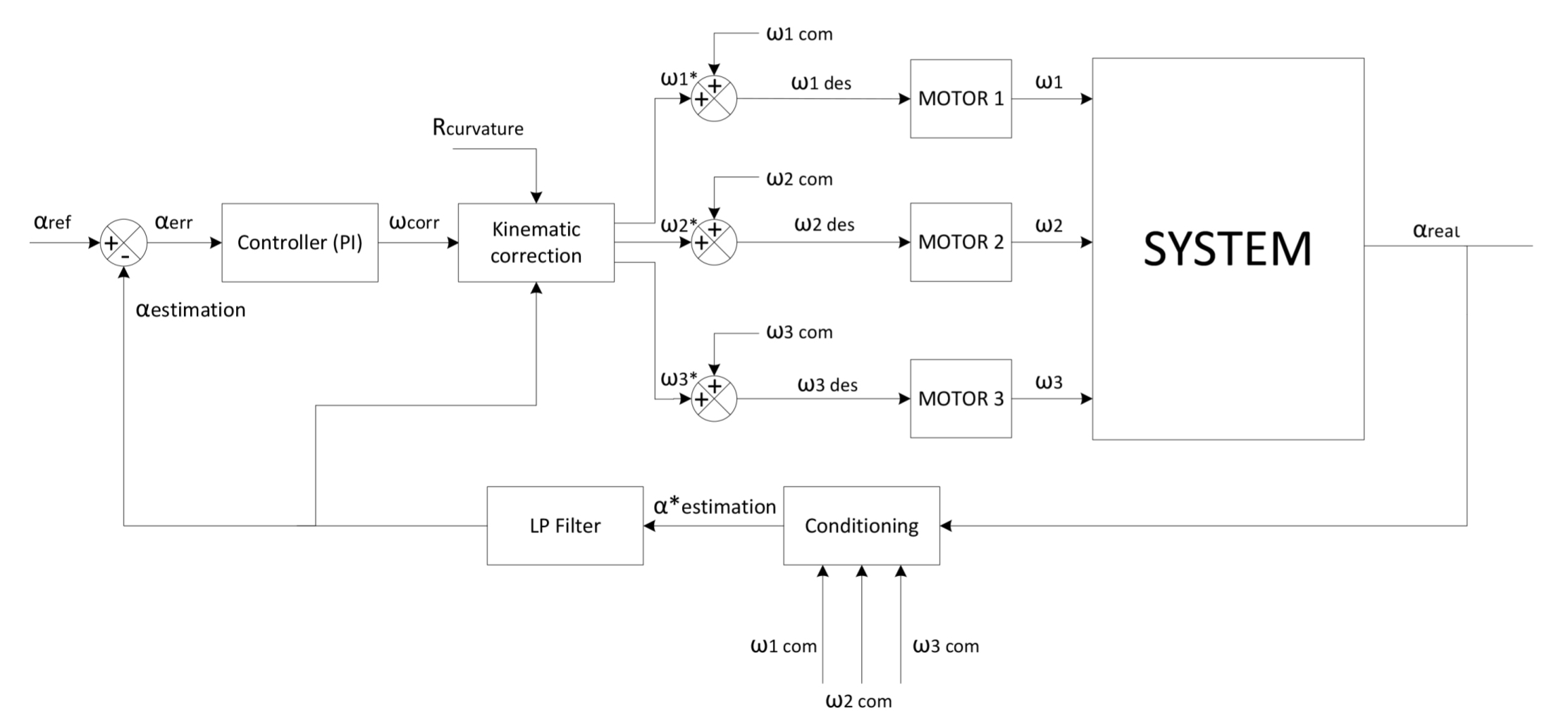
Closed loop control diagram.

Snapshots from the Omniclimber experiments on a pole of 220mm diameter, without and with the new controller. Moving vertically parallel to the pole axis.